原题干:
As an emergency rescue team leader of a city, you are given a special map of your country. The map shows several scattered cities connected by some roads. Amount of rescue teams in each city and the length of each road between any pair of cities are marked on the map. When there is an emergency call to you from some other city, your job is to lead your men to the place as quickly as possible, and at the mean time, call up as many hands on the way as possible.
Input
Each input file contains one test case. For each test case, the first line contains 4 positive integers: N (<= 500) - the number of cities (and the cities are numbered from 0 to N-1), M - the number of roads, C1 and C2 - the cities that you are currently in and that you must save, respectively. The next line contains N integers, where the i-th integer is the number of rescue teams in the i-th city. Then M lines follow, each describes a road with three integers c1, c2 and L, which are the pair of cities connected by a road and the length of that road, respectively. It is guaranteed that there exists at least one path from C1 to C2.
Output
For each test case, print in one line two numbers: the number of different shortest paths between C1 and C2, and the maximum amount of rescue teams you can possibly gather.
All the numbers in a line must be separated by exactly one space, and there is no extra space allowed at the end of a line.
Sample Input
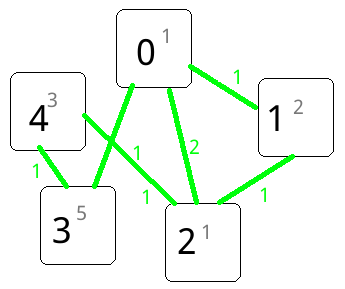
5 6 0 2 1 2 1 5 3 0 1 1 0 2 2 0 3 1 1 2 1 2 4 1 3 4 1
Sample Output
2 4
大意:救援队规划最短路线。第一行给出城市数量、道路数量、起点、目的地
接着第二行给出每个城市中包含的救援小组的数量(点权)
接下来给出所有道路的距离,格式为"城市甲 城市乙 甲乙距离"(边权)
要求规划出最短路径,并输出最短路径的条数(有几种最短路径方案)和路途能获得的最大救援小组数量
样例图:
这道题只是一个很简单的Dijkstra算法问题。但是一定在Dijkstra函数的更新数组部分要细心,稍不留神就会出错(博主这道题有一个变量弄反了,找错找了一白天。。。)
对Dijkstra算法多路径求解的思路不了解的同学看这里:Dijkstra算法进阶--多条最短路径情况
代码如下:
#include <iostream>
#include <algorithm>
using namespace std;
#define MAXN 510
#define INF 0x3fffffff
int G[MAXN][MAXN], PointWeight[MAXN] = {0};
int StartP, EndP, PointNum, RoadNum;
int MaxWeight[MAXN] = {0}, RoadCnt[MAXN] = {0};
int MinDistance[MAXN];
bool Visited[MAXN] = {false};
void Dijkstra(int s){
//init
fill(MinDistance, MinDistance + MAXN, INF);
MaxWeight[s] = PointWeight[s];
RoadCnt[s] = 1;
MinDistance[s] = 0;
for(int i = 0; i < PointNum; i++){
//find MIN Distance ponit
int p = -1, MIN = INF;
for(int j = 0; j < PointNum; j++){
if(Visited[j] == false && MinDistance[j] < MIN){
p = j,
MIN = MinDistance[j];
}
}
if(p == -1) return;
//found
Visited[p] = true;
//Use Point-p as medi-point to Update Point-j
for(int j = 0; j < PointNum; j++){
if(G[p][j] != INF && Visited[j] == false){
//if find a better way
if(G[p][j] + MinDistance[p] < MinDistance[j]){
MinDistance[j] = G[p][j] + MinDistance[p];
RoadCnt[j] = RoadCnt[p];
MaxWeight[j] = MaxWeight[p] + PointWeight[j];
}
//if find a alike way
else if(G[p][j] + MinDistance[p] == MinDistance[j]){
RoadCnt[j] += RoadCnt[p];
if(MaxWeight[j] < MaxWeight[p] + PointWeight[j])
MaxWeight[j] = MaxWeight[p] + PointWeight[j];
}
}
}
}
}
int main(){
cin >> PointNum >> RoadNum >> StartP >> EndP;
//Read PointWeight
for(int i = 0; i < PointNum; i++)
cin >> PointWeight[i];
//init G
fill(G[0], G[0] + MAXN * MAXN, INF);
//Read Graph
for(int i = 0; i < RoadNum; i++){
int _, __;
cin >> _ >> __;
cin >> G[_][__];
G[__][_] = G[_][__];
}
Dijkstra(StartP);
//Output Result
cout << RoadCnt[EndP] << " " << MaxWeight[EndP] << endl;
return 0;
}