0x00、从迷宫说起
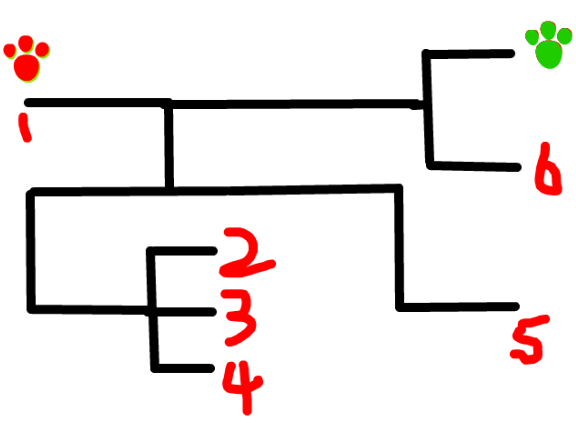
假设你现在处于一个这样的巨大的迷宫中,没有通讯工具,没有上帝视角,无法激活巴拉拉正能量,只能靠自己,从红色的脚印走到绿色的脚印,你会怎么走?
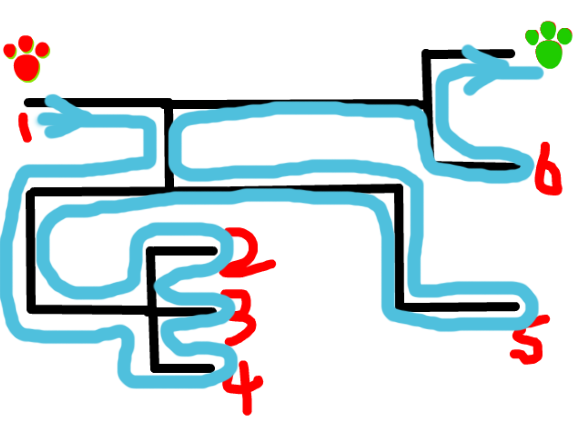
相信你的答案一定是正确的。在没有地图的情况下,走出去的最好的方式一定是:在1点,始终保持右手靠着墙壁,一直前进,一定就会走到终点。
在1点出发,走到第一个岔路口,然后要保证右手靠墙,我们就向下走,接着下一个岔路口向左走,然后又是一个岔路口,走到4,发现是死胡同,保证右手靠墙的原地返回,走向3,2,...然后返回上一层岔路口,层层查找。
我们把这种搜索终点的方式称之为"深度优先搜索,简称DFS(Depth First Search)"
0x01、深度优先搜索的实现
从起点,走向第一层岔道,在第一层岔道内部搜索,然后进入第一层岔道内部的岔道,走到了死胡同再返回第一层岔道,走向第二层岔道。。。
写到这里可能很多人会听出来了,这个和我们前面说过的"栈"很类似,因为先进入的岔道一定会先出来,符合栈的"先进先出"法则。
但是这里我们可以用递归来实现,递归的时候系统会调用系统栈,也算是间接使用了栈。
0x02、解决一个实际问题试试
假设我是一个卖货的老大爷,我有n种货物,每件货物质量为weight[i],价值为cost[i],我现在需要选择若干件货物放在一个最大承重为V的包包里,使得包中物品价值最大,求最大价值
解决这道题前我们先把它和迷宫问题联系在一起。
这里每件物品都有选中与不选中两种可能,这就相当于迷宫中的"岔道口"。而物品总量不得超过V,这就是迷宫中的死胡同。
所以每次都要对物品进行排序,排序的起点是数组下标为0的位置,所以得到函数原型:
void DFS(int index, int sumW, int sumC);
//这里index为正在处理的位置。sumW为当前总质量,sumC为当前总价值我们定义一个全局变量,MaxValue,让每次到"死胡同"时,计算价值与MaxValue进行比较,如果大,则替换。反之,则返回
//死胡同情况
if(index == n){ //已经完成了对n件货物的全部处理,相当于死胡同
if(sumW <= V) //必须要使得总质量比最大承重小
if(sumC > MaxValue) //如果大,则替换
MaxValue = sumC;
return; //死胡同,返回。
}岔道口我们有两种选择,选中并加上质量和价值,或者不选中,什么也不加,代码如下:
DFS(index+1, sumW, sumC);
//index+1表示处理下一件,sumW和sumC表示下标为index的货物没被选中
DFS(index+1, sumW+weight[index], sumC+cost[index]);
//index+1表示处理下一件,后两个参数加上了本间物品的价值与质量,表示本件物品被选中了全部代码如下:
#include <iostream>
using namespace std;
int n, V, MaxValue = 0;
int weight[100], cost[100];
void DFS(int index, int sumW, int sumC){
//如果是死胡同
if(index == n){
if(sumW <= V && sumC > MaxValue) MaxValue = sumC;
return;
}
//如果是岔路口
DFS(index + 1, sumW, sumC);
DFS(index + 1, sumW + weight[index], sumC + cost[index]);
}
int main(){
cout << "输入物品数量和包的最大承重:";
cin >> n >> V;
for(int i = 0; i < n; i++){
cout << "输入第" <<i<< "件物品的重量和价值";
cin >> weight[i] >> cost[i];
}
DFS(0, 0, 0); //初始值是下标为0的物品,初始重量和初始价值均为0
cout << "最大价值为:" << MaxValue << endl;
return 0;
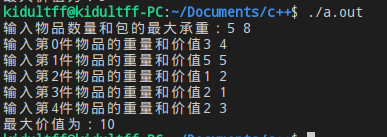
}运行结果: