题干:
字符串APPAPT中包含了两个单词"PAT",其中第一个PAT是第2位(P),第4位(A),第6位(T);第二个PAT是第3位(P),第4位(A),第6位(T)。
现给定字符串,问一共可以形成多少个PAT?
输入格式:
输入只有一行,包含一个字符串,长度不超过105,只包含P、A、T三种字母。
输出格式:
在一行中输出给定字符串中包含多少个PAT。由于结果可能比较大,只输出对1000000007取余数的结果。
输入样例:
APPAPT
输出样例:
2
乍一眼一看挺简单,写了如下的代码:
#include <cstdio>
#include <cstring>
int main(void){
char str[100100];
long long cnt = 0;
const int MOD = 1000000007;
scanf("%s",&str);
int len = strlen(str);
/*计算开始*/
for(int p = 0; p < len; p++){
if(str[p] != 'P') continue; //找P,如果不是P,下一个
for(int a = p; a < len; a++){
if(str[a] != 'A') continue; //找A,如果不是A,下一个
for(int t = a; t < len; t++) {
if(str[t] == 'T') cnt++;
}
}
}
/*计算结束,输出*/
printf("%lld",cnt % MOD);
return 0;
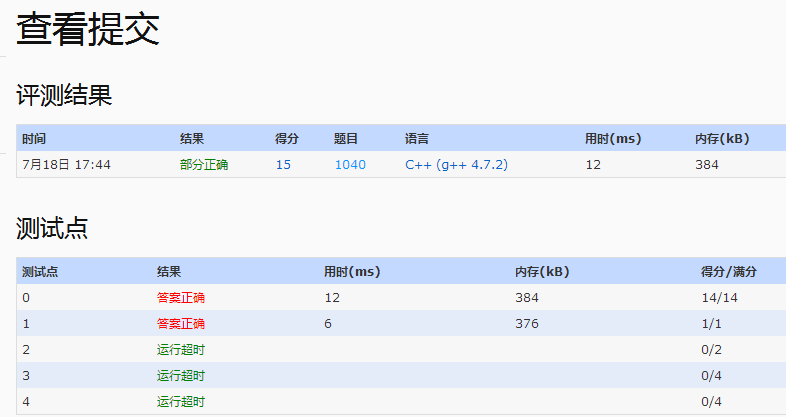
}提交到PAT,如果不出意料,出现的是下面的结果:
这是由于过多次的遍历,导致做了很多重复的动作,所以会超时。
换种思维考虑,我们可以计算A左边的P的个数,再算A右边T的个数,一一将P与T组合,就可以得到答案了,而且只遍历了两次次数组,时间复杂度为O(2strlen)。当然你可以只遍历一次,并将左边的P与右边的T的个数计入数组,时间复杂度更低,为O(2strlen),不过代码略复杂。这里给出前种的代码。PAT完美通过。
#include <cstdio>
#include <cstring>
/* APATTPATTAT */
int main(void){
char str[100100];
int l_p = 0, r_t = 0;
long long cnt = 0;
const int MOD = 1000000007;
scanf("%s",&str);
int len = strlen(str);
for(int i = 0; i < len; i++){
if(str[i] == 'T') r_t++; //计算总共有多少T
}
/*计算开始*/
for(int i = 0; i < len; i++){
if(str[i] == 'P') l_p++; //左P++
if(str[i] == 'T') r_t--; //右T--
if(str[i] == 'A') cnt += l_p * r_t; //遇到A就计算一次
}
/*计算结束,输出*/
printf("%lld",cnt % MOD);
return 0;
}