0x00、概述
我们都学过数组的遍历,把数组所有元素都访问一遍,就称之为数组的遍历。同理,将二叉树的所有元素都访问一遍,也称之为二叉树的遍历。
二叉树的遍历一般分为4种:先序、中序、后序、层次。前面三种可以使用DFS来实现,层次遍历可以使用BFS实现。
说道DFS会想到死胡同和岔路口,遍历到叶子节点就是死胡同了,而岔路口有两条路可供选择:lchild和rchild,即左节点和右节点。在习惯上,我们要先遍历左节点,后遍历右节点。
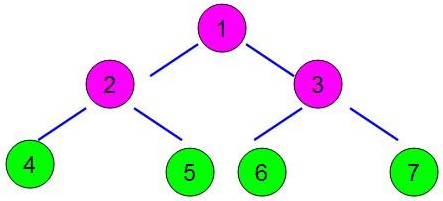
在下面的描述中,我们会用这棵二叉树举例子:
好了,下面我们来看看先序遍历。
0x01、先序遍历
先序遍历是一种很好理解的遍历方式,一般来说先序遍历的访问顺序为根节点->左子树->右子树。
我们可以用一个简单的递归来实现:
/*二叉树先序遍历,传入二叉树节点指针类型(node*)的root根节点指针*/
void preorder(node* root){ //preorder为先序遍历的英文名称
if(root == NULL) //说明正在访问的是叶子节点,死胡同
return;
printf(root->data); //输出本次访问的节点的数据域数据
preorder(root->lchild);
preorder(root->rchild); //递归访问左右节点
}在二叉树内部的访问情况:(二叉树见上图)
1,根节点是1,它的地址不会是NULL,输出1的数据,访问1的左节点(lchild),也就是2。此时的输出为{1}
2,2的地址不是NULL,输出2的数据,访问4。此时的输出为{1, 2}
|- 3,4的地址不是NULL,输出4的数据,访问4的左节点,也就是NULL,返回。此时的输出为{1, 2, 4}
|- 4,访问4的右节点,也就是NULL
|- 5,NULL的地址是NULL,返回。对4的访问结束。此时的输出为{1, 2, 4}
6,访问2的右节点5,输出5的数据,接着访问5的左右节点,都是NULL,对2的访问结束。
此时的输出为{1, 2, 4, 5}。
7,对3进行访问。。。。。。巴拉巴拉巴拉巴拉
最终输出结果为 1,2,4,5,3,6,7
先序遍历序列的特征为:{树根、左子树、右子树}
0x02、中序遍历
中序遍历其实就是换了下顺序,我们先访问左子树,在访问数据域,最后访问右子树。
根据前序遍历我们只需要修改一下顺序,同样可以很轻松的写出访问算法:
void inorder(node* root){
if(root == NULL)
return;
inorder(root->lchild);
printf(root->data);
inorder(root->rchild);
}在二叉树内部的访问情况:(二叉树见上图)
1,根节点是1,它的地址不会是NULL,访问1的左节点(lchild),也就是2。
2,2的地址不是NULL,访问2的左节点4。
|- 3,4的地址不是NULL,访问4的左节点,也就是NULL,返回
|- 4,输出4的数据域,此时的输出为 {4}
|- 5,访问4的右节点,NULL,返回。对4的访问结束。此时的输出为{4}
6,输出2的数据域部分,此时的输出为{4, 2}。
7,访问2的右节点5。输出5。此时的输出为{4, 2, 5}
。。。。。巴拉巴拉巴拉巴拉
最终输出结果为 4,2,5,1,6,3,7
中序遍历序列的特征为:{左子树、树根、右子树}
0x03、后序遍历
同样,只是颠倒了个顺序而已。。。先访问左节点,再访问右节点,最后访问数据域,就叫后序遍历。
C语言实现:
void postorder(node* root){
if(root == NULL)
return;
postorder(root->lchild);
postorder(root->rchild);
printf(root->data);
}在二叉树内部的访问情况:(二叉树见上图)
1,根节点是1,它的地址不会是NULL,访问1的左节点(lchild),也就是2。
2,2的地址不是NULL,访问2的左节点4。
|- 3,4的地址不是NULL,访问4的左节点,也就是NULL,返回
|- 4,访问4的右节点,NULL,返回。
|- 5,输出4的数据域,对4的访问结束。此时的输出为 {4}。
6,访问2的右节点5。输出5。此时的输出为 {4, 5}。
7,输出2的数据域部分,此时的输出为{4, 5, 2}。
。。。。。巴拉巴拉巴拉巴拉
最终输出结果为 4, 5, 2, 6, 7, 3, 1
后序遍历序列的特征为:{左子树、右子树、树根}
0x04、层序遍历
层序遍历与上面三种遍历不一样。层序遍历的特征是根据层级进行访问。从根节点开始,一层一层的遍历。同一层的元素要从左往右遍历。
上面三种在遍历期间体现了先进后出的原则,所以我们利用递归时调用的系统栈,使用DFS算法即可遍历。而层级遍历要去层层遍历,先遍历到的父节点先输出,体现了先进先出原则,我们可以利用队列,使用BFS算法实现。
void LayerOrder(node* root){
queue<node*> q; //注意,队列中存放的是根节点,根节点要用地址来表示
q.push(root); //将根节点压入队列
while(!q.empty()){ //队列非空的时候不断处理。直到队列为空
node* now = q.front(); //now在这里起到迭代器的作用,表示正在处理的节点。
q.pop(); //下面开始处理队首,将队首弹出队列
printf(now->data);
if(!now->lchild) q.push(now->lchild); //左子列非空,将左子列压入队列,末尾,排队处理
if(!now->rchild) q.push(now->rchild); //右子列非空,将右子列压入队列,末尾,排队处理
}
}在二叉树内部的访问情况:(二叉树见上图)
1,根节点是1,将1压入队列此时队列为{1}
2,迭代器now=1,队首1出队,输出1的数据,将1的左右节点(2,3)压入队列,此时队列为{2,3},输出为{1}
3,迭代器now=2,队首2出队,输出2的数据,将2的左右节点(4,5)压入队列,此时队列为{3,4,5},输出为{1,2}
4,迭代器now=3,队首3出队。。。。。。。
。。。。。巴拉巴拉巴拉巴拉。。
最终输出结果为 1,2,3,4,5,6,7
如果我们想要知道二叉树的具体层次,我们可以在结构体中定义一个层次变量,来表示当前节点所处于的层次:
struct node{
int data;
int layer; //层次
node* lchild;
node* rchild;
};遍历的时候将层次写入节点即可
下面是一段样例代码:
void LayerOrderWithLayerNum(node* root){
queue<node*> q;
root->layer = 1; //根节点为1
q.push(q);
while(q.empty()){
node* now = q.front(); //迭代器
q.pop();
printf(now->data);
if(!now->lchild){
now->lchild->layer = now->layer + 1; //写入层级
q.push(now->lchild);
}
if(!now->rchild){
now->rchild->layer = now->layer + 1; //写入层级
q.push(now->rchild);
}
}
}0x05、根据遍历结果序列,重建二叉树
还有一个重要的问题:给出某棵二叉树的先序遍历和中序遍历的序列,然后重建这棵二叉树。
例如给出先序序列:{1,2,4,5,3,6,7},和中序序列{4,2,5,1,6,3,7},要求你还原这棵二叉树
我们知道,先序序列的第一个值一定是二叉树的根,所以二叉树的根的data为1。{1,2,4,5,3,6,7}
由于中序序列中,根节点将二叉树划分为左子树和右子树,所以我们下一步找中序序列中,为1的值{4,2,5,1,6,3,7}
1左边的元素为左子树,右边的元素为右子树。{4,2,5,1,6,3,7}
所以左子树的个数为3,右子树个数为3。同时得出了左子树和右子树在先序序列中序列区间,分别是[1,3]和[4,6]
以此类推,使用递归重建二叉树即可。
当循环到先序序列区间长度为0的时候,递归就结束了。
下面我们尝试用C语言实现这个步骤:
/*创建还原二叉树函数,preL和preR为先序序列区间,inL和inR为中序序列区间。返回根节点地址*/
node* create(int preL, int preR, int inL, int inR){
if(preL > preR) return NULL; //先序序列长度<=0的时候,递归结束
node* root = new node; //创建新节点,存放二叉树根节点
root->data = pre[preL]; //根节点的数值为先序序列的第一个值
int k; //k用来存储根节点的位置下标
for(k = inL; k <= inR; k++){
if(in[K] == pre[preL]) break; //在中序序列中找到根节点的位置
}
int numLeft = k - inL; //左子树节点个数等于中序序列起始位置到中序序列中节点的位置
/*根节点的左子树的先序序列区间为[preL+1, preL+numLeft]
这是因为preL的位置存放的是根节点的数据,从它下一个,往后推numLeft大小,就是左子树
根节点的左子树的中序序列区间为[inL, k-1]
这是因为中序序列中,根节点位置的左边都是左子序列*/
root->lchild = create(preL+1, preL+numLeft, inL, k - 1)
/*根节点的右子树的先序序列区间为[preL+numLeft+1, preR]
这是因为先序序列存放左子树序列的后面的所有都是右子树
根节点的右子树的中序序列区间为[inL, k-1]
这是因为中序序列中,根节点位置的右边都是右子序列*/
root->rchild = create(preL+numLeft+1, preR, k+1, inR);
return root;
}

非常有帮助,十分感谢分享!