原题干:
给定一段一段的绳子,你需要把它们串成一条绳。每次串连的时候,是把两段绳子对折,再如下图所示套接在一起。这样得到的绳子又被当成是另一段绳子,可以再次对折去跟另一段绳子串连。每次串连后,原来两段绳子的长度就会减半。
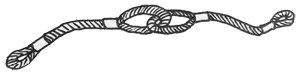
给定N段绳子的长度,你需要找出它们能串成的绳子的最大长度。
输入格式:
每个输入包含1个测试用例。每个测试用例第1行给出正整数N (2 <= N <= 104);第2行给出N个正整数,即原始绳段的长度,数字间以空格分隔。所有整数都不超过104。
输出格式:
在一行中输出能够串成的绳子的最大长度。结果向下取整,即取为不超过最大长度的最近整数。
输入样例:
8 10 15 12 3 4 13 1 15
输出样例:
14
这道题很简单嘛。。。完全就是一个考察算法的问题,每次与其他的绳子连接的时候自己都会减半,所以只要先去连接短的绳子,就可以让跟着减半的部分都是那些短绳子,长绳子被减半的次数会很少。这样就达到了题目要求。
代码如下:
#include <bits/stdc++.h>
using namespace std;
int main(){
int cnt;
cin >> cnt;
vector<int> v(cnt);
for(int & i : v) cin >> i;
sort(v.begin(), v.end());
int ans = v[0];
for(int i = 1; i < v.size(); i++){
ans += v[i];
ans /= 2;
}
cout << ans << endl;
return 0;
}
