0x00、复杂多条最短路径问题
前面我们提到过多条最短路径类问题,诸如"新增边权"、"新增点权"、"求最短路径条数(新增计数器)"等类问题,这里面新增的内容被我们称为"第二标尺"。(传送门:多条最短路径情况)
在多条最短路径类问题上,一般的出题套路会围绕着"和"来探讨,例如让新增边权之和最小,新增点权之和最大,路径条数最小等等。但是不排除问题不单纯的让求"和",这时问题会变得比较复杂,用之前的方式就无法得到正确的结果,因为题目不一定要求满足最优子结构。下面介绍一种Dijkstra+DFS的思路来解决这种逻辑较为复杂的问题
Dijkstra+DFS的思路很好理解,在之前的解决方案里,我们遵循"发现最短路径就更新,发现相同路径就比较第二标尺并累加",而使用Dijkstra+DFS的思路是"在Dijkstra算法里面记录下所有的最短路径,然后使用DFS遍历所有路径,选出第二标尺最优的路径"。下面具体说说该如何实现
0x01、Dijkstra生成前驱数组
先说说Dijkstra求解出的最短路径怎么输出吧!首先引入前驱数组的定义:
前驱数组,就是 数组的 每个元素 都存放着 元素代表的节点 的前驱
如果只是存放单个前驱,我们定义一个一维数组做为前驱数组就好了
int pre[MAXN];在编写Dijkstra函数的时候,我们要在更新数组的部分稍作修改:
if(发现以u做中介点,走向v,可以获得更好的路径){
pre[u] = v; //记录前驱
存放最短距离数组[v] = 存放最短距离数组[v] + 邻接矩阵[u][v];
}接着我们在Dijkstra运行完毕后就可以使用DFS算法输出这条最短路径经历了哪些节点了:
void DFS(int p){
if(p == 起点){ //起点是递归边界,这是因为我们从终点往前遍历。
//从终点往前遍历最方便,这是因为我们数组里保存的都是前驱
printf(起点);
return;
}
DFS(pre[p]); //如果p不是递归边界,我们递归遍历p的前驱
printf(p);
}
DFS(终点); //DFS入口以上就是只记录一条路径的情况下,怎么使用DFS+前驱数组输出路径,下面看看记录多个路径的情况
这里我们的前驱不能使用一维数组了,因为我们要记录多个路径就可能产生多个前驱。我们使用变长数组vector
vector<int> pre[MAXN];这样pre数组的每个单元都可以存放多个值,对于每一个节点v而言,就可以存放v的所有能产生最短路径的前驱结点。
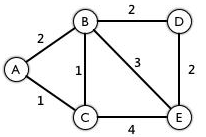
比如说下面的这个图,现在要求找到 A 点到 E 点的最短路径:
我们的pre数组内部存储是这样的:
pre[A] = {A};
pre[B] = {A,C};
pre[C] = {A};
pre[D] = {B};
pre[E] = {B,C};我们使用DFS遍历这个数组,就可以获得全部最短路径:
{A, B, E}、{A, C, E}、{A, C, B, E}
在Dijkstra算法中,你可以无需看第二标尺,专心求解前驱数组。里面更新数组思路为:
if(发现距离更短的路径){
更新存放最短路径的数组;
清空这个点对应的前驱数组;
将这个点存入前驱数组
}else if(发现距离相同的路径){
将这个点存入前驱数组
}其他的思路与一般Dijkstra算法一样。
用C语言实现就是:
vector<int> pre[MAXN];
void Dijkstra(int s){ //s为起点
fill(d, d + MAXN, INF); //d为存放最短路径值的数组,INF为一个很大的数
d[s] = 0; //初始化d[s]
for(int i = 0; i < n; i++){ //n为顶点个数。
/*开始找路径最短的点*/
int u = -1, MIN = INF; //u为下表,MIN为存放路径最短的值
for(int j = 0; j < n; j++)
if(visited[j] == false && d[j] < MIN)
u = j, MIN = d[j];
if(u == -1) return;
visited[u] = true;
for(int v = 0; v < n; v++){ //枚举每一个点
if(visited[v] == false && G[u][v]!=INF){ //并更新有路可走而且没有遍历过的
if(d[u] + G[u][v] < d[v]){
d[v] = d[u] + G[u][v];
pre[v].clear();
pre[v].push_back(u);
}else if(d[u] + G[u][v] == d[v]){
pre[v].push_back(u);
}
}
}
}
}这样,我们就完成了前驱数组的创建。接着我们使用DFS,在路径最短的条件下找到使第二标尺。
0x02、DFS找到最优路径
前面说过了前驱数组,下面我们要做的就是使用DFS遍历前驱数组,找到第二标尺最优的路径。
DFS算法最大的特征是递归,递归函数一般分为两部分:递归边界和递归式,那么我们这里面的递归边界和递归式分别是什么呢?
很显然,我们从终点开始遍历(因为我们保存的是前驱数组。所以必须从终点开始遍历),遍历到起点就是递归边界了;而递归式,把当前访问的节点对应的vector容器遍历一遍,每一个节点都递归一次就好啦
代码如下:
int bestValue; //存放第二标尺最优值
vector<int> pre[MAXN]; //前驱节点数组
vector<int> path; //存放最优路径
vector<int> tempPath; //存放临时路径
void DFS(int v){ //v为当前访问的节点
tempPath.push_back(v); //将v加入临时路径
//DFS的"死胡同",递归边界
if(v == startPoint){ //遍历到了终点
int value; //在此计算第二标尺
if(value比bestValue更优){ //比较当前第二标尺与之前最优的第二标尺,确定是不是一条更优的路径
bestValue = value; //更新最优值
path = tempPath; //更新最优路径
}
}
//DFS的"岔路口",递归式
else{ //v != startPoint,没遍历到终点
for(int i = 0; i < pre[v].size(); i++){//枚举容器内的所有前驱结点
DFS(pre[v][i]); //然后依次遍历
}
tempPath.pop_back(); //本节点找完了,删掉。以便遍历其他的
}