0x00、二叉查找树的递归定义
二叉查找树(二叉搜索树、二叉排序树、排序二叉树、Binary Search Tree,BST)是一种特殊的二叉树。递归定义如下:
●若二叉查找树没有任何节点,则二叉查找树为空树
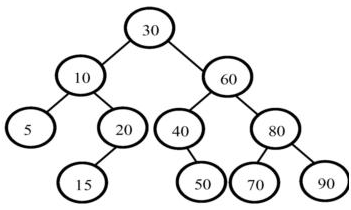
●若二叉查找树不是空树,则二叉查找树的左子树和右子树均为二叉树,而且左节点的数据域小于等于根节点,右节点的数据域大于根节点。如下图
0x01、二叉查找树的查找操作(C语言实现)
因为二叉查找树的左右节点与根节点的大小关系是固定的,所以查找起来不像普通二叉树一样,"盲目"的查找。
我们可以确定这样的一个思路。比如要寻找数字:n,根节点为root。
●如果root == NULL则查找失败,返回
●如果root->data == n则查找成功,输出
●如果root->data < n,说明要查找的数据比当前节点大,应该往右找
●如果root->data > n,说明要查找的数据比当前节点小,应该往左找
下面我们尝试使用C语言递归代码实现查找函数:
/**
* 二叉查找树的递归查找方法
* 传入根节点root和要查找的数据data
*/
void search(node* root, int data){
if(root == NULL)return; //查找失败
if(root -> data == data) //查找成功
printf("%d", root -> data);
if(root -> data > data) //当前节点大,往左找
search(node -> lchild, data);
if(root -> data < data) //当前节点小,往右找
search(node -> rchild, data);
}0x02、插入操作
二叉查找树是有顺序的,所以插入操作不可以像普通二叉树一样,"盲目"的插入,要根据顺序插入到正确的位置,我们按照下面的思路插入节点。比如根节点为root,要插入的数据为data
●如果root == null,这里就是应该插入的位置,让root=new node,并写入数据data
●如果root->data == data,那么说明数据已经存在了,返回
●如果root->data < data,说明数据比根节点大,往右搜索合适位置并插入
●如果root->data > data,说明数据比根节点小,往左搜索合适位置并插入
下面我们尝试使用C语言实现二叉查找树的插入过程:
void insert(node* &root, int data){
if(root == NULL){ //节点为空,插入到当前节点
root = new node;
root->lchild = NULL, root->rchild = NULL;
root->data = data;
return;
}
if(root -> data == data) //数据已存在,无需插入
return;
else if(root -> data < data)//比节点数据大,往右插
insert(root->rchild, data);
else if(root -> data > data)//比节点数据小,往左插
insert(root->lchild, data);
}上面代码中,参数部分node* &root,这里加&是因为函数里面可能修改了root,如果不加&就不会真正修改。
0x03、二叉搜索树的中序遍历
二叉搜索树有个很实用的性质,由于二叉搜索树的特性:左子树<根节点<右子树,这和中序遍历的顺序是一样的,所以二叉搜索树的中序遍历序列就是一个有顺序的序列。
0x04、删除操作
我们依然拿这个二叉搜索树举例:
假如我现在想要删掉节点30,如果直接删除,把节点30给free掉,后果是二叉树被分成两部分,不再是一棵完整的二叉树,所以我们不可以直接删除节点。
这里定义两个定义:
在一个集合中,存在n属于这个集合。比n小的最大的数叫做n的前驱;比n大的最小的数叫做n的后继。
例如上面的二叉搜索树,30的前驱是20;30的后继是40。
接着我们继续回归到我们之前的问题上,删除节点30。
由于二叉树中序遍历是有顺序的,所以我们有两种删除30的方法:
1,我们可以使用30的前驱:20,替换掉30,接着问题转化为删除子树20。删除20的时候我们用20的前驱:15,替换掉20的位置,这样就成功删除了30.
2,我们可以使用30的后继:40,替换掉30,接着问题转化为删除子树40。删除40的时候我们使用40的后继:50,替换掉40,这样就删除了40.
所以这仍然是一个递归问题!删除某个节点的时候使用后继或前驱替换掉节点,然后再以前驱或后继作为根节点删除下一级的前驱或后继,从而完成二叉搜索树删除节点。
下面我们先来实现查找根节点的前驱和后继。
查找前驱的时候也就是查找根节点左节点的最大值,我们只需要以左节点做为根节点,沿着右边遍历一遍即可。问题转化为找最大值,代码如下:
node* findMax(node* root){
while(root->rchild != NULL)
root = root->rchild; //不断往右(大)
return root;
}同理,找最小值:
node* findMin(node* root){
while(root->lchild != NULL)
root = root->lchild; //不断往右(大)
return root;
}下面来完成删除节点的完整的函数:
void deleteNode(node* &root, int data){
if(root == NULL) return; //不存在这个点
if(root->data == data){ //找到了
if(root->lchild == NULL && root->rchild == NULL) //叶子节点直接删除
root = NULL; //删除
else if(root->lchild != NULL){
node* pre = findMax(root->lchild); //在左子树中找到最大值,也就是root的前驱
root->data = pre->data; //使用前驱的数据覆盖掉根节点的数据
deleteNode(root->lchild, pre->data); //删掉前驱
//(因为前驱数据已经给了根节点。再保留前驱就重复了)
}else if(root->rchild != NULL){
node* next = findMin(root->rchild); //右子树找最小值,也就是root的后继
root->data = next->data;
deleteNode(root->rchild, next->data);
}
}else if(root->data != data){ //这个点不是要删除点
if(root->data > data) //当前点大了。往左边瞅瞅
deleteNode(root->lchild, data);
if(root->data < data) //当前点笑了,往右边瞅瞅
deleteNode(root->rchild, data);
}
}