哈利·波特要考试了,他需要你的帮助。这门课学的是用魔咒将一种动物变成另一种动物的本事。例如将猫变成老鼠的魔咒是haha,将老鼠变成鱼的魔咒是hehe等等。反方向变化的魔咒就是简单地将原来的魔咒倒过来念,例如ahah可以将老鼠变成猫。另外,如果想把猫变成鱼,可以通过念一个直接魔咒lalala,也可以将猫变老鼠、老鼠变鱼的魔咒连起来念:hahahehe。
现在哈利·波特的手里有一本教材,里面列出了所有的变形魔咒和能变的动物。老师允许他自己带一只动物去考场,要考察他把这只动物变成任意一只指定动物的本事。于是他来问你:带什么动物去可以让最难变的那种动物(即该动物变为哈利·波特自己带去的动物所需要的魔咒最长)需要的魔咒最短?例如:如果只有猫、鼠、鱼,则显然哈利·波特应该带鼠去,因为鼠变成另外两种动物都只需要念4个字符;而如果带猫去,则至少需要念6个字符才能把猫变成鱼;同理,带鱼去也不是最好的选择。
输入格式:
输入说明:输入第1行给出两个正整数N (≤100)和M,其中N是考试涉及的动物总数,M是用于直接变形的魔咒条数。为简单起见,我们将动物按1~N编号。随后M行,每行给出了3个正整数,分别是两种动物的编号、以及它们之间变形需要的魔咒的长度(≤100),数字之间用空格分隔。
输出格式:
输出哈利·波特应该带去考场的动物的编号、以及最长的变形魔咒的长度,中间以空格分隔。如果只带1只动物是不可能完成所有变形要求的,则输出0。如果有若干只动物都可以备选,则输出编号最小的那只。
输入样例:
6 11 3 4 70 1 2 1 5 4 50 2 6 50 5 6 60 1 3 70 4 6 60 3 6 80 5 1 100 2 4 60 5 2 80
输出样例:
4 70
这道题是一道最短路径的问题。这里我使用了遍历节点,对每个节点使用Dijkstra算法过一遍,然后找到最长路径。再比较。
样例输入示意图:
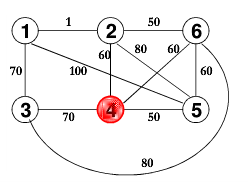
样例的最短路径表如下
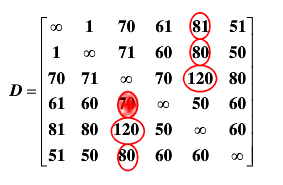
代码如下:
#include <iostream>
#include <algorithm>
using namespace std;
#define MAXN 101
#define INF 0x3fffffff
int G[MAXN][MAXN], cnt_c, cnt_s;
int ans_id = INF, ans_len = INF;
bool Dijkstra(int s){
bool visited[MAXN] = {false};
int d[MAXN];
fill(d, d + MAXN, INF);
d[s] = 0; //自己到自己的距离为0
//Dijkstra
for(int i = 1; i <= cnt_c; i++){ //对于每一个点
int p = -1, min = INF;
for(int j = 1; j <= cnt_c; j++){
if(visited[j] == false && d[j] < min){
p = j, min = d[j];
}
}
if(p == -1) return false;
visited[p] = true;
for(int v = 1; v <= cnt_c; v++){
if(visited[v] == false && G[p][v] != INF && d[p] + G[p][v] < d[v])
d[v] = d[p] + G[p][v];
}
}
//找距离最长的
int MinDis = -1;
for(int i = 1; i <= cnt_c; i++){
if(d[i] > MinDis){
MinDis = d[i];
}
}
//覆盖结果
if(ans_len > MinDis){
ans_id = s, ans_len = MinDis;
}else if(ans_len == MinDis && s == ans_id){
ans_id = s;
}
return true;
}
int main(){
cin >> cnt_c >> cnt_s;
fill(G[0], G[0] + MAXN * MAXN, INF);
for(int i = 0; i < cnt_s; i++){
int _1, _2, _len;
cin >> _1 >> _2 >> _len;
G[_1][_2] = G[_2][_1] = _len;
}
for(int i = 1; i <= cnt_c; i++){
if(Dijkstra(i) == false){
cout << 0 << endl;
return 0;
}
}
cout << ans_id << ' ' << ans_len << endl;
return 0;
}
