0、距离
在直角坐标系中,平面两个点之间的距离为
将其拓展到三维,在根号里加上个(z0-z1)的平方即可。据此,很容易将距离拓展到n维。
将一个样本的n个特征看作是n维空间上的一个点,点的坐标值就是(X0,X1,...,Xn)
这样就可以求出两个样本之间的距离。
1、KNN
对于新来的点,对其分类时,需要计算这个新样本与其他样本的距离,并找到与它距离最近的N个点。N可以取3,5,7...不取偶数是因为怕“平局”,即和两个类别的点距离最近的个数一样,这样就无法判断了。
使用sklearn,对鸢尾花数据集进行KNN分类:
from sklearn import neighbors
from sklearn import datasets
knn = neighbors.KNeighborsClassifier()
iris = datasets.load_iris()
knn.fit(iris.data, iris.target)对一个新样本点进行预测:
knn.predict([[0.1, 0.2, 0.3, 0.4]])得到预测结果:
array([0])
2、KNN的不足
例如有下面的样本:
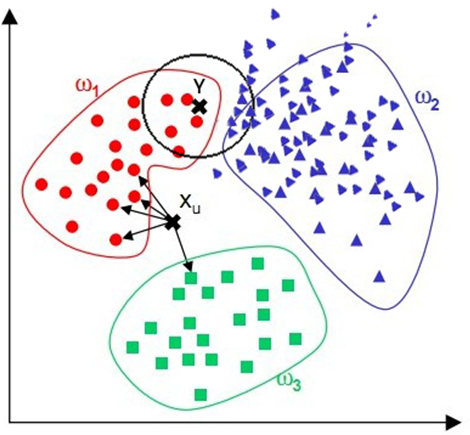
对Y点进行预测时,肉眼可见它属于ω1类,但是使用KNN时,如果N=11,由于它和ω2的点距离近的更多,会将其错误的归为ω2类。
对于这样的问题,可以在计算距离时,加上一个1/n作为权重,即总数分之一,这样样本总量过多的类别的点的权重将被弱化,从而解决了问题。

