Given a tree, you are supposed to tell if it is a complete binary tree.
Input Specification:
Each input file contains one test case. For each case, the first line gives a positive integer N (≤20) which is the total number of nodes in the tree -- and hence the nodes are numbered from 0 to N−1. Then N lines follow, each corresponds to a node, and gives the indices of the left and right children of the node. If the child does not exist, a - will be put at the position. Any pair of children are separated by a space.
Output Specification:
For each case, print in one line YES and the index of the last node if the tree is a complete binary tree, or NO and the index of the root if not. There must be exactly one space separating the word and the number.
Sample Input 1:
9 7 8 - - - - - - 0 1 2 3 4 5 - - - -
Sample Output 1:
YES 8
Sample Input 2:
8 - - 4 5 0 6 - - 2 3 - 7 - - - -
Sample Output 2:
NO 1
题目大意:第一行给一个小于等于20的数字N,表示给定二叉树的节点个数。接着给出N行,每行给两个值,第一个值表示左孩子,第二个表示右孩子。数字表示编号,“-”表示不存在。问给定的树是不是一棵完全二叉树。
这道题我调试了将近5个小时,不断的出错。。。
首先思路不能错,要明确完全二叉树的定义,看下图:
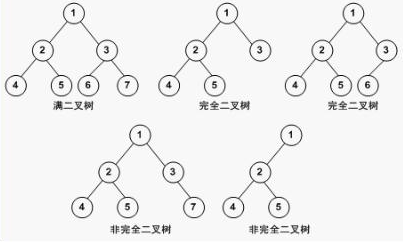
注意下面的第一个不是完全二叉树,所以不能用层序遍历再求每一层的个数来判断是不是完全二叉树。
这是一个因思路错误造成的经典错解:
void layerOrder(int s){
//max_layer为最大层,layer为每层存放的节点个数,last为最后一个节点
int max_layer = 0, layer[MAXN] = {0}, last = s;
queue<int> Q;
Q.push(s);
//层序遍历的bfs算法
while(!Q.empty()){
int top = Q.front();
last = top; //最后一个节点肯定最后一个遍历到
Q.pop();
if(T[top].lchild != -1){ //左孩子存在
T[ T[top].lchild ].layer = T[top].layer + 1; //层次+1
Q.push(T[top].lchild);
}
if(T[top].rchild != -1){ //右孩子存在
T[ T[top].rchild ].layer = T[top].layer + 1;
Q.push(T[top].rchild);
}
//更新最大层次
if(T[top].layer > max_layer) max_layer = T[top].layer;
//每一层有多少个节点的计数器++
layer[T[top].layer]++;
}
int i;
//判断是否每一层达到了2^(i-1)个节点
for(i = 1; i <= max_layer; i++)
if(layer[i] != pow(2, i-1))
break;
i >= max_layer的时候,说明都满足了
if(i >= max_layer)
cout << "YES " << last << endl;
else cout << "NO " << s << endl;
}如果用层序遍历的方式来写这道题,必须要加个判断,判断总共出现了几个“瘸腿的”节点(只有一个孩子)。如果出现了只有右孩子的,直接ban,如果出现了多个只有左孩子的,依然ban。但是这种思路不是最简单的,下面有更简单的思路。
还要注意一点,虽然给的样例输入的节点号都是一位的,但是节点号不一定是一位的!20以内的数字都可以,所以不能用一个char来读取!必须用char[]或者string!!
由char造成的段错误、答案错误经典错解:
char c;
cin >> c;
if(c == '-') return -1;
return c - '0';最简单的思路:使用先序遍历,同时记录节点在树中的下标,找到最大下标,如果最大下标比节点数量要大,说明前面一定有残缺的。
使用递归比较简单。代码:
#include <iostream>
#include <algorithm>
#include <string>
using namespace std;
#define MAXN 100
typedef struct{
int lchild, rchild;
} node;
node T[MAXN]; //静态二叉树
//have:存放输入中出现了的节点。cnt:存放节点个数。max_idx:存放最大下标。last:存放最后一个节点
int have[MAXN] = {0}, cnt, max_idx = -1, last = 0;
int GetChild(){
string c;
cin >> c;
if(c == "-") return -1;
have[stoi(c)] = 1;
return stoi(c);
}
int GetRoot(){
for(int i = 0; i < cnt; i++)
if(have[i] == 0) return i;
}
void preOrder(int root, int idx){
if(root == -1) return;
if(idx > max_idx){
max_idx = idx;
last = root;
}
preOrder(T[root].lchild, idx * 2);
preOrder(T[root].rchild, idx * 2 + 1);
}
int main(){
cin >> cnt;
for(int i = 0; i < cnt; i++){
T[i].lchild = GetChild();
T[i].rchild = GetChild();
}
int root = GetRoot();
preOrder(root, 1);
if(max_idx == cnt) cout << "YES " << last;
else cout << "NO " << root;
cout << endl;
return 0;
}
