PAT-A 真题 – 1123 Is It a Complete AVL Tree

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

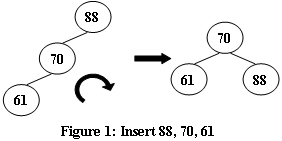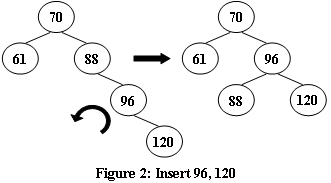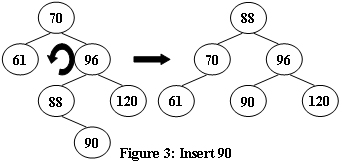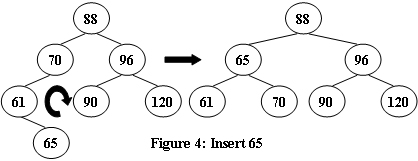Now given a sequence of insertions, you are supposed to output the level-order traversal sequence of the resulting AVL tree, and to tell if it is a complete binary tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N ( $\leq$ 20). Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, insert the keys one by one into an initially empty AVL tree. Then first print in a line the level-order traversal sequence of the resulting AVL tree. All the numbers in a line must be separated by a space, and there must be no extra space at the end of the line. Then in the next line, print YES if the tree is complete, or NOif not.

Sample Input 1:

5
88 70 61 63 65

Sample Output 1:

70 63 88 61 65
YES

Sample Input 2:

8
88 70 61 96 120 90 65 68

Sample Output 2:

88 65 96 61 70 90 120 68
NO

题目大意：给定一些数字，插入到AVL树中，输出AVL树的层序遍历序列，并判断插入后的AVL树是否为完全二叉树。

对于AVL树，老老实实的插入就好了。不会AVL树操作的点这里：https://www.mmuaa.com/post/c94f085f14aed644.html

对于判断是否是完全二叉树，方法就是在层序遍历的时候加上节点号，像堆那样，加上下标，根节点的下标为1，判断最后一个点的下标是否和节点总量相等，相等的话就是完全二叉树。

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <vector>
#include <queue>
#include <cmath>
using namespace std;

struct node{
  int data, height;
  node *lchild, *rchild;
};
typedef struct{  //带下标的BFS 
    node* root;
    int idx;
} _node;

int GetHeight(node *root){
  return root == NULL ? 0 : root->height;
}

int GetBalance(node *root){
  return GetHeight(root->lchild) - GetHeight(root->rchild);
}

void UpdateHeight(node *root){
  root->height = max(GetHeight(root->lchild), GetHeight(root->rchild)) + 1;
}

void LL(node* &root){
  node *tmp = root->lchild;
  root->lchild = root->lchild->rchild;
  tmp->rchild = root;
  UpdateHeight(root);
  UpdateHeight(tmp);
  root = tmp;
}

void RR(node* &root){
  node *tmp = root->rchild;
  root->rchild = root->rchild->lchild;
  tmp->lchild = root;
  UpdateHeight(root);
  UpdateHeight(tmp);
  root = tmp;
}

void LR(node* &root){
  RR(root->lchild);
  LL(root);
}

void RL(node* &root){
  LL(root->rchild);
  RR(root);
}

void insert(int n, node* &root){
  if(root == NULL){
    root = new node;
    root->data = n;
    root->lchild = root->rchild = NULL;
    root->height = 1;
  }
  else{
    if(root->data > n)  //往左插入
      insert(n, root->lchild);
    else
      insert(n, root->rchild);
    UpdateHeight(root);  //更新树高 
    if(GetBalance(root) == 2)  //旋转 
      if(GetBalance(root->lchild) == 1) LL(root);
      else LR(root); 
    else if(GetBalance(root) == -2)
      if(GetBalance(root->rchild) ==-1) RR(root);
      else RL(root);
  }
}

int BFS(node* root, vector<int> &layer){
  int index = 0;
  queue<_node> Q;
  Q.push({root, 1});
  while(!Q.empty()){
    _node Qfront = Q.front();
    node* root = Qfront.root;
    index = Qfront.idx;
    layer.push_back(root->data);
    Q.pop();
    if(root->lchild) Q.push({root->lchild, index * 2});  //左子树下标为2*根节点下标 
    if(root->rchild) Q.push({root->rchild, index * 2 + 1});  //右子树下标为2*根节点下标+1 
  }
  return index;
}

int main(){
  int cnt;
  cin >> cnt;
  node *root = NULL;
  for(int i = 0; i < cnt; i++){
    int tmp;
    cin >> tmp;
    insert(tmp, root);
  }
  vector<int> layer;
  int max_idx = BFS(root, layer);  //有多少层
  for(int i = 0; i < layer.size(); i++){
    if(i) cout << ' ';
    cout << layer[i];
  }
  cout << endl;
  //完全二叉树最大下标应该和总节点数一致 
  if(max_idx != cnt) cout << "NO" << endl;
  else cout << "YES" << endl; 
  return 0;
}

斐斐のBlog